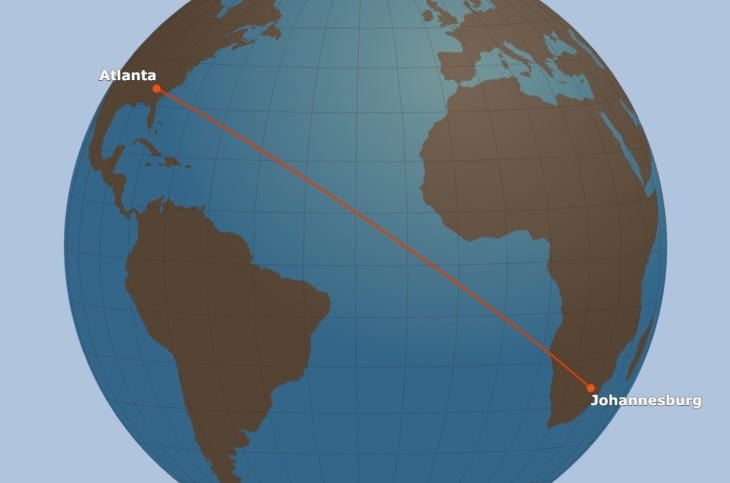
In navigation, we sometimes face an awkward fact of life that many people don’t give too much thought to–our charts are flat, but the earth is round. If you’re flying a Cessna between Miami and Orlando, it doesn’t much matter. But it matters a lot if you’re plotting a course from Singapore to New York!
Planes and ships crossing oceans must use the great-circle distance when planning their trip. This is the shortest distance between two points on the surface of a sphere. When plotted on the standard aeronautical chart, the course will appear curved. But when projected onto a globe, the course is obviously the shortest route.
Air Navigation Introduction
Let’s start by reviewing how we typically deal with courses and distance in aviation, particularly basic pilot training.
The typical aeronautical chart is a Mercator Projection, which means that the earth’s curved surface is distorted, so it can be presented on a flat piece of paper (or a flat screen, if you will). To make this happen, mapmakers keep the meridians–the lines of longitude–parallel to one another. But if you look at a globe, meridians are not parallel–they converge on one another at the poles.
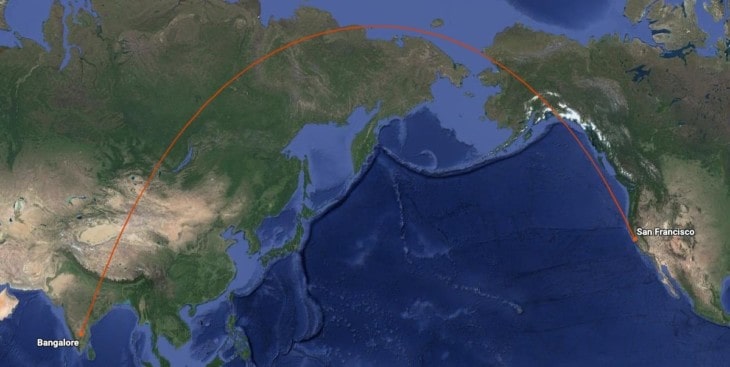
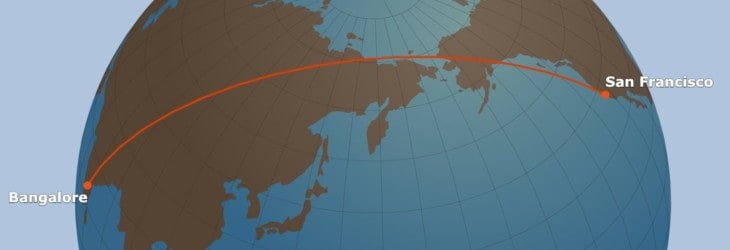
When a pilot pulls out their chart and draws a line between their departure point and destination, they are drawing a rhumb line.
But we know that the earth’s surface is not flat, and if you plotted this course on a globe, it would not make sense. It’s fine if you are traveling only a short distance, but if you are crossing continents and oceans, you must be more accurate. In these cases, you’d want to use the great-circle distance.
Measuring Distances
Distance is simply the measurement of how far apart two points are. For example, you might measure two points on a piece of paper in millimeters, centimeters, or inches. On the highway, you might measure the distance between two towns in statue miles or kilometers.
In the air or on the sea, you measure the distance between two points in nautical miles. If you compare statute miles vs nautical miles, you’ll find that nautical miles are slightly larger at about 1.15 statute miles for every nautical mile.
Measuring distances on an aeronautical chart is easy, and there are several ways to do it. The best is with a plotter, a plastic tool that allows you to measure distance like a standard ruler. The plotter has markings for the three common chart scales (sectionals, world aeronautic chart, and terminal aeronautic charts).
Great Circle Distance Explained
Measuring with paper charts and plotters works fine for short trips. But the curve of the earth must be accounted for on longer flights.
“Great circle” is a term from spherical trigonometry, sometimes called an orthodrome. It is defined as the circular intersection of a sphere caused by a plane* passing through the sphere’s center point. *A plane as in a two-dimensional surface from geometry, not an airplane.
When you measure distances along the great circle, they will always be the shortest distance between those two points. A sphere can have an infinite number of great circles drawn, and they can be drawn in any direction. But a great circle will always divide the sphere into two equal halves.
The key for navigation is that your great circle must be drawn through the center of the earth, your departure point, and your destination.
Those paying attention in science class may recall that the earth is not a perfect sphere. Rather, it is an oblate ellipsoid–a slightly flattened sphere. However, there are formulas to account for this difference to make great circle routes even more accurate.
What Is a Great Circle vs Small Circle?
A small circle is similar to the great circle described above, but the plane DOES NOT intersect the sphere’s center point. That means that the two divided parts of the sphere are unequal.
A small circle differs from a great circle, and the distance measured between the points does not equal the shortest distance.
Great Circle Routes vs Rhumb Line Routes
Both great circle routes and rhumb lines are used in aviation, and each has pluses and minuses.
Great circle routes are also called “orthodromic routes.” These routes measure the shortest distance between two points on a sphere, so they are used when taking trips of 1,000 nautical miles or more.
But great circle routes are complicated. You can’t easily measure, plot, or fly them. When drawn on a standard Mercator Projection chart, they intersect each meridian (line of longitude) at a different angle. In practice, that means that to fly them accurately, you’d have to adjust your heading continuously while flying.
A rhumb line is sometimes called a “loxodromic route.” In contrast to the great circle, a rhumb line is easy to draw, plot, and measure on a standard chart. It intersects each meridian at the same angle. That means that in the plane, you can fly the compass heading to your destination the entire way.
Unfortunately, as easy as the rhumb line is to fly, it is less efficient than a great circle route when flying long distances. It is not the shortest distance between two points, so it will take longer to get to your destination than it needs to, and you’ll use more fuel.
Other Limitations on Routes
Before modern computer navigation, great circle routes were flown by dividing the route up with several waypoints and creating rhumb lines that connected each waypoint. That way, the total route was more or less a great circle, but each leg was simply flown as a rhumb line.
Modern electronic navigation equipment like GPS can calculate the great circle route and fly it, changing the plane’s heading along the way.
But, even with these modern technologies, most flights are not flying perfect great circles. Whether on VFR or IFR flight plans, flights are still limited to predetermined air traffic routes.
You can think of those routes as breaking up a great circle into legs, with waypoints along the way. And each leg can then be flown as a rhumb line with a constant heading.
The result is that transcontinental and transoceanic flights do follow something that is, at the very least, close to a great circle route.
Great Circle Distance Calculator Tools
Calculating great circle routes is one of the most involved math formulas in aviation or navigation. It’s called the haversine formula, and it involves cosigns, tangents, and a mess of square roots. In short, you had better have gotten an A+ in trigonometry back in school. And it’s well beyond the scope of this article.
But, for those still with us and looking to get some numbers, there are a few calculators on the web that can help. In addition, most modern flight planning software apps will consider great circle distances.
Best Great Circle Distance Calculator with Waypoints
Planet Calc has a great tool that will calculate a great circle route and give you the distance, initial course, final course, and waypoints in between.
Great Circle Distance Calculator Nautical Miles
The FAA’s great circle distance calculation tool lets you input any two points (latitude and longitude) and gives you the distance measured in feet, miles, nautical miles, meters, and kilometers.
Shortest Distance Between Two Points on Earth Formula Calculator
Omni Calculator Distance Tool does the same but includes corrections for the more accurate ellipsoid distances.
Related Posts
- Mayday Call: Diving Into This Vital Distress Signal
- Headwinds vs Tailwinds: What's the Difference for Pilots?
- What is a Bush Pilot and how to become one
About the Author
